压缩态可以写成
其中, 为平移算符,
为压缩算符. 平移算符中的平移参数 满足 . 其证明如下 一般情况下 和
是不同的.
上式说明从制备压缩态的角度, “先平移后压缩” 和 “先压缩后平移”
可以得到同一个压缩态. 此处不同的写法对应着不同的位移参数 和 , 那么为什么通常我们更关心 的实部和虚部? 为了说明这件事,
首先广义坐标和广义动量, 其分别为
在 和 对应的相空间中, 规定 为相空间的横轴, 为相空间的纵轴,
压缩态的示意图如下图所示. 图中的紫色图像是量子态的误差椭圆,
代表着量子态, 第一个量子态是真空态, 因此误差椭圆是一个圆, 其位置在原点.
压缩算符 先作用真空态上,
误差椭圆由圆变成了椭圆, 平移算符 再作用上去,
在相空间中产生了一段位移, 估计的参数是这段位移. 这段位移起点在原点,
终点是压缩态
的误差椭圆的中心点, 也即坐标和动量的期望 . 在压缩态 下可以计算得到 以及 , 因此有压缩态下有
以及 ,
这正是为什么我们构造这样的估计问题.
 压缩态
压缩态
注意 和 的关系, 这意味着在 和 形成的相空间中, 态
的位移并不是位移参数 ,
而对于相干态
在相空间中的位移是 ,
这说明压缩算符作用到非真空态上, 其实使其产生了位移. 为了分析这件事,
首先分析压缩算符 ,
其采取的定义为
将压缩算符分解为
其中 . 下面来证明式 . 上述结果中并不含 , 将
代入压缩算符表达式中, 这样出现了 的形式, 而分解后的 指数上不再有 指数. 在量子光学的算符运算中时常用到
, 其中 是 的函数, 是幺正算符. 利用这一点, 中指数上的指数,
可以通过一个指数形式的算符变成三个一阶指数相乘的形式. 以此我们来证明式
. 注意到 是幺正矩阵, 且 . 分析 的性质, 有如下结果
因此式
的右式可写为
是一个旋转算符, 结合式
说明沿某个角度
的压缩可以分解成先将坐标系旋转 , 再沿坐标系压缩,
再旋转回原坐标系. 根据压缩算符的作用效果,
我们来看压缩算符作用在真空态和相干态上有何不同.
我们将算符的作用统一视为作用在空间上, 以一个 的网格表示相空间,
其原点坐标中心处. 压缩算符作用在真空态的空间时如下图所示.
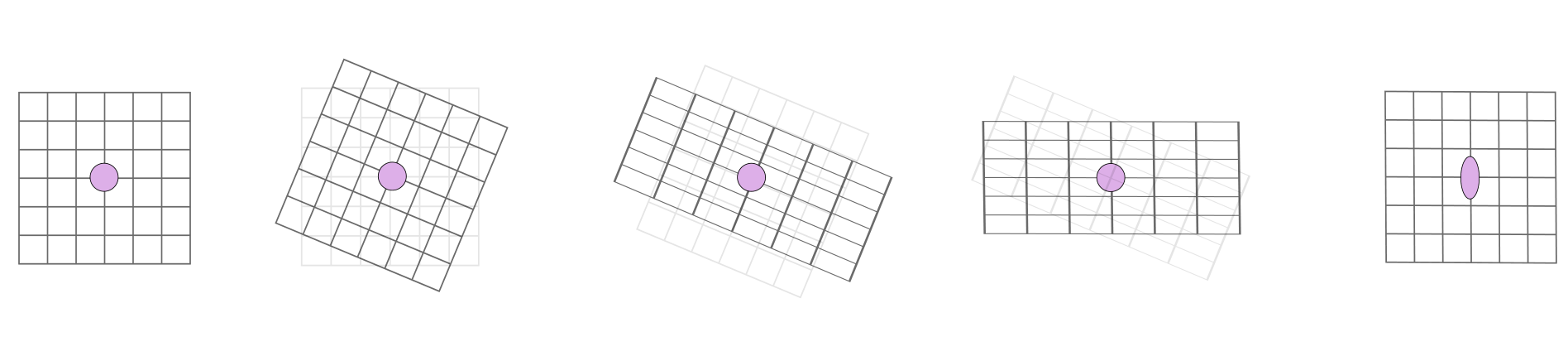
可以看到无论 和 如何选取, 都不会有位移产生.
压缩算符作用在相干态的空间时上, 如下图所示,

由上图可以看出, 在旋转中产生了一段位移, 由于经历了压缩,
旋转同样的角度的位移已经不一样了, 在 “转回去” 的操作中,
这段位移并不会完全抵消. 这个有趣的事实也是论文 “Quantum amplification of
mechanical oscillator motion ” 的关键.

